Hypothesis testing have been extensively used on different discipline of science. And in this post, I will attempt on discussing the basic theory behind this, the Likelihood Ratio Test (LRT) defined below from Casella and Berger (2001), see reference 1.
Example 1. Let X_1,X_2,\cdots,X_n\overset{r.s.}{\sim}f(x|\theta)=\frac{1}{\theta}\exp\left[-\frac{x}{\theta}\right],x>0,\theta>0. From this sample, consider testing H_0:\theta = \theta_0 vs H_1:\theta<\theta_0.
Solution:
The parameter space \Theta is the set (0,\Theta_0], where \Theta_0=\{\theta_0\}. Hence, using the likelihood ratio test, we have \lambda(\mathbf{x})=\frac{\displaystyle\sup_{\theta=\theta_0}L(\theta|\mathbf{x})}{\displaystyle\sup_{\theta\leq\theta_0}L(\theta|\mathbf{x})},
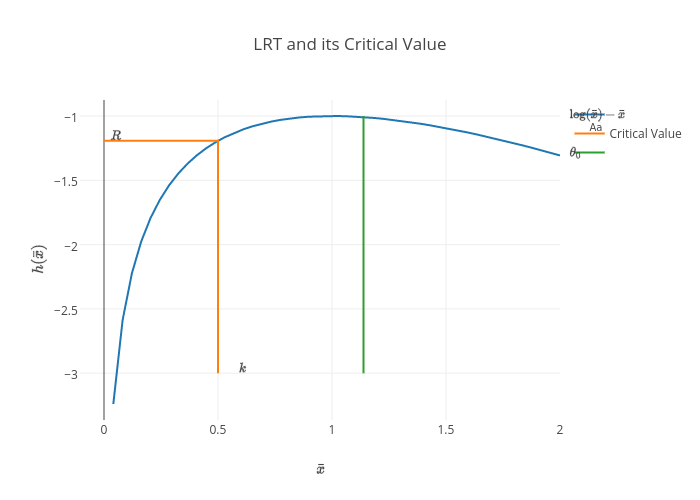
So that, \begin{aligned} \lambda(\mathbf{x})&=\frac{\left(\frac{1}{\theta_0}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta_0}\right]} {\left(\frac{1}{\bar{x}}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\bar{x}}\right]},\quad\text{provided that}\;\bar{x}\leq \theta_0\\ &=\left(\frac{\bar{x}}{\theta_0}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta_0}\right]\exp[n]. \end{aligned}
Above figure is the plot of h(\bar{x}) function with \theta_0=1. Given the assumption that \bar{x}\leq \theta_0 then assuming R=\frac{1}{n}\log c-1 designates the orange line above, then we reject H_0 if h(\bar{x})\leq R, if and only if \bar{x}\leq k. In practice, k is specified to satisfy,
\mathrm{P}(\bar{x}\leq k|\theta=\theta_0)\leq \alpha,
It follows that X_i|\theta = \theta_0\overset{r.s.}{\sim}\exp[\theta_0], then \mathrm{E}X_i=\theta_0 and \mathrm{Var}X_i=\theta_0^2. If \bar{x}=\frac{1}{n}\sum_{i=1}^{n}X_i and if G_n is the distribution of \frac{(\bar{x}_n-\theta_0)}{\sqrt{\frac{\theta_0^2}{n}}}. By CLT (central limit theorem) \lim_{n\to\infty}G_n converges to standard normal distribution. That is, \bar{x}|\theta = \theta_0\overset{r.s.}{\sim}AN\left(\theta_0,\frac{\theta_0^2}{n}\right). AN - assymptotically normal.
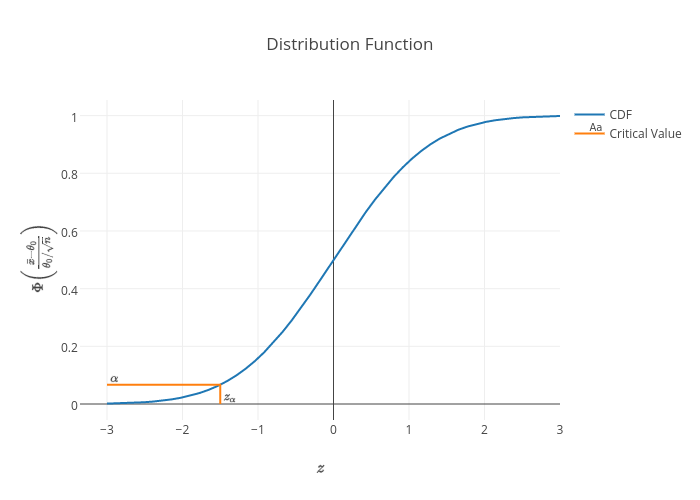
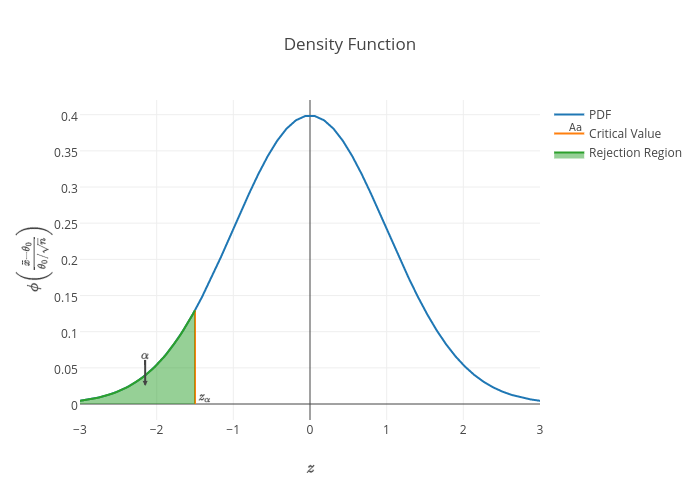
Thus, \mathrm{P}(\bar{x}\leq k|\theta=\theta_0)=\Phi\left(\frac{k-\theta_0}{\theta_0/\sqrt{n}}\right),\quad\text{for large }n.
with corresponding PDF given by,
Implying,
\frac{k-\theta_0}{\theta_0/\sqrt{n}}=z_{\alpha}\Rightarrow k=\theta_0+z_{\alpha}\frac{\theta_0}{\sqrt{n}}.
Definition. The likelihood ratio test statistic for testing H_0:\theta\in\Theta_0 versus H_1:\theta\in\Theta_0^c is \begin{equation} \label{eq:lrt} \lambda(\mathbf{x})=\frac{\displaystyle\sup_{\theta\in\Theta_0}L(\theta|\mathbf{x})}{\displaystyle\sup_{\theta\in\Theta}L(\theta|\mathbf{x})}. \end{equation}The numerator of equation (\ref{eq:lrt}) gives us the supremum probability of the parameter, \theta, over the restricted domain (null hypothesis, \Theta_0) of the parameter space \Theta, that maximizes the joint probability of the sample, \mathbf{x}. While the denominator of the LRT gives us the supremum probability of the parameter, \theta, over the unrestricted domain, \Theta, that maximizes the joint probability of the sample, \mathbf{x}. Therefore, if the value of \lambda(\mathbf{x}) is small such that \lambda(\mathbf{x})\leq c, for some c\in [0, 1], then the true value of the parameter that is plausible in explaining the sample is likely to be in the alternative hypothesis, \Theta_0^c.A likelihood ratio test (LRT) is any test that has a rejection region of the form \{\mathbf{x}:\lambda(\mathbf{x})\leq c\}, where c is any number satisfying 0\leq c \leq 1.
Example 1. Let X_1,X_2,\cdots,X_n\overset{r.s.}{\sim}f(x|\theta)=\frac{1}{\theta}\exp\left[-\frac{x}{\theta}\right],x>0,\theta>0. From this sample, consider testing H_0:\theta = \theta_0 vs H_1:\theta<\theta_0.
Solution:
The parameter space \Theta is the set (0,\Theta_0], where \Theta_0=\{\theta_0\}. Hence, using the likelihood ratio test, we have \lambda(\mathbf{x})=\frac{\displaystyle\sup_{\theta=\theta_0}L(\theta|\mathbf{x})}{\displaystyle\sup_{\theta\leq\theta_0}L(\theta|\mathbf{x})},
where,
\begin{aligned}
\sup_{\theta=\theta_0}L(\theta|\mathbf{x})&=\sup_{\theta=\theta_0}\prod_{i=1}^{n}\frac{1}{\theta}\exp\left[-\frac{x_i}{\theta}\right]\\
&=\sup_{\theta=\theta_0}\left(\frac{1}{\theta}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta}\right]\\
&=\left(\frac{1}{\theta_0}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta_0}\right],
\end{aligned}
and
\begin{aligned}
\sup_{\theta\leq\theta_0}L(\theta|\mathbf{x})&=\sup_{\theta\leq\theta_0}\prod_{i=1}^{n}\frac{1}{\theta}\exp\left[-\frac{x_i}{\theta}\right]\\
&=\sup_{\theta\leq\theta_0}\left(\frac{1}{\theta}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta}\right]=\sup_{\theta\leq\theta_0}f(\mathbf{x}|\theta).
\end{aligned}
Now the supremum of f(\mathbf{x}|\theta) over all values of \theta\leq\theta_0 is the MLE (maximum likelihood estimator) of f(x|\theta), which is \bar{x}, provided that \bar{x}\leq \theta_0.
So that, \begin{aligned} \lambda(\mathbf{x})&=\frac{\left(\frac{1}{\theta_0}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta_0}\right]} {\left(\frac{1}{\bar{x}}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\bar{x}}\right]},\quad\text{provided that}\;\bar{x}\leq \theta_0\\ &=\left(\frac{\bar{x}}{\theta_0}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta_0}\right]\exp[n]. \end{aligned}
And we say that, if \lambda(\mathbf{x})\leq c, H_0 is rejected. That is,
\begin{aligned}
\left(\frac{\bar{x}}{\theta_0}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta_0}\right]\exp[n]&\leq c\\
\left(\frac{\bar{x}}{\theta_0}\right)^n\exp\left[-\displaystyle\frac{\sum_{i=1}^{n}x_i}{\theta_0}\right]&\leq c',\quad\text{where}\;c'=\frac{c}{\exp[n]}\\
n\log\left(\frac{\bar{x}}{\theta_0}\right)-\frac{n}{\theta_0}\bar{x}&\leq \log c'\\
\log\left(\frac{\bar{x}}{\theta_0}\right)-\frac{\bar{x}}{\theta_0}&\leq \frac{1}{n}\log c'\\
\log\left(\frac{\bar{x}}{\theta_0}\right)-\frac{\bar{x}}{\theta_0}&\leq \frac{1}{n}\log c-1.
\end{aligned}
Now let h(x)=\log x - x, then h'(x)=\frac{1}{x}-1. So the critical point of h'(x) is x=1. And to test if this is maximum or minimum, we apply second derivative test. That is,
h''(x)=-\frac{1}{x^2}<0,\forall x.
Thus, x=1 is a maximum. Hence,
\log\left(\frac{\bar{x}}{\theta_0}\right)-\frac{\bar{x}}{\theta_0}
is maximized if \frac{\bar{x}}{\theta_0}=1\Rightarrow\bar{x}=\theta_0. To see this consider the following plot,
where \alpha is called the level of the test.
It follows that X_i|\theta = \theta_0\overset{r.s.}{\sim}\exp[\theta_0], then \mathrm{E}X_i=\theta_0 and \mathrm{Var}X_i=\theta_0^2. If \bar{x}=\frac{1}{n}\sum_{i=1}^{n}X_i and if G_n is the distribution of \frac{(\bar{x}_n-\theta_0)}{\sqrt{\frac{\theta_0^2}{n}}}. By CLT (central limit theorem) \lim_{n\to\infty}G_n converges to standard normal distribution. That is, \bar{x}|\theta = \theta_0\overset{r.s.}{\sim}AN\left(\theta_0,\frac{\theta_0^2}{n}\right). AN - assymptotically normal.
Thus, \mathrm{P}(\bar{x}\leq k|\theta=\theta_0)=\Phi\left(\frac{k-\theta_0}{\theta_0/\sqrt{n}}\right),\quad\text{for large }n.
So that,
\mathrm{P}(\bar{x}\leq k|\theta=\theta_0)=\Phi\left(\frac{k-\theta_0}{\theta_0/\sqrt{n}}\right)\leq \alpha.
Plotting this gives us,
Therefore, a level-\alpha test of H_0:\theta=\theta_0 vs H_1:\theta<\theta_0 is the test that rejects H_0 when \bar{x}\leq\theta_0+z_{\alpha}\frac{\theta_0}{\sqrt{n}}.
Plot's Python Codes
In case you might ask how above plots were generated:
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| ##------------------------------## | |
| # LRT AND ITS CRITICAL VALUE # | |
| ##------------------------------## | |
| import plotly.plotly as py | |
| from plotly.graph_objs import * | |
| import numpy as np | |
| def f1(x): | |
| return np.log(x) - x | |
| trace1 = Scatter( | |
| x = np.linspace(0, 2), | |
| y = f1(np.linspace(0, 2)), | |
| name = "\\log(\\bar{x})-\\bar{x}" | |
| ) | |
| trace2 = Scatter( | |
| x = [0, 0.5], | |
| y = [f1(0.5), -3], | |
| name = "Critical Value", | |
| mode = "lines+text", | |
| text = ["\;R", "\;k"], | |
| textposition = 'top right', | |
| textfont = Font( | |
| family = "sans serif", | |
| ), | |
| line = Line( | |
| shape = 'hv' | |
| ) | |
| ) | |
| trace3 = Scatter( | |
| x = [1, 1], | |
| y = [-3, -1], | |
| name = "\\theta_0", | |
| mode = "lines", | |
| line = Line( | |
| shape = 'vh' | |
| ) | |
| ) | |
| layout = Layout( | |
| title = "LRT and its Critical Value", | |
| xaxis = XAxis( | |
| title = "\\bar{x}" | |
| ), | |
| yaxis = YAxis( | |
| title = "h(\\bar{x})" | |
| ) | |
| ) | |
| data = Data([trace1, trace2, trace3]) | |
| fig = Figure(data = data, layout = layout) | |
| plot_url = py.plot(fig, filename = 'lrt') | |
| ##-------------------------## | |
| # DISTRIBUTION FUNCTION # | |
| ##-------------------------## | |
| import plotly.plotly as py | |
| from plotly.graph_objs import * | |
| import numpy as np | |
| from scipy.stats import norm | |
| trace1 = Scatter( | |
| x = np.linspace(-3, 3), | |
| y = norm.cdf(np.linspace(-3, 3)), | |
| name = "CDF" | |
| ) | |
| trace2 = Scatter( | |
| x = [-3, -1.5], | |
| y = [norm.cdf(-1.5), 0], | |
| name = "Critical Value", | |
| mode = "lines+text", | |
| text = ["\\;\\alpha", "\\;z_{\\alpha}"], | |
| textposition = 'top right', | |
| textfont = Font( | |
| family = "sans serif", | |
| ), | |
| line = Line( | |
| shape = 'hv' | |
| ) | |
| ) | |
| layout = Layout( | |
| title = "Distribution Function", | |
| xaxis = XAxis( | |
| title = "z" | |
| ), | |
| yaxis = YAxis( | |
| title = "\\Phi\\left(\\frac{\\bar{x}-\\theta_0}{\\theta_0/\\sqrt{n}}\\right)" | |
| ) | |
| ) | |
| data = Data([trace1, trace2]) | |
| fig = Figure(data = data, layout = layout) | |
| plot_url = py.plot(fig, filename = 'cdf') | |
| ##--------------------## | |
| # DENSITY FUNCTION # | |
| ##--------------------## | |
| import plotly.plotly as py | |
| from plotly.graph_objs import * | |
| import numpy as np | |
| from scipy.stats import norm | |
| trace1 = Scatter( | |
| x = np.linspace(-3, 3), | |
| y = norm.pdf(np.linspace(-3, 3)), | |
| name = "PDF" | |
| ) | |
| trace2 = Scatter( | |
| x = [-1.5, -1.5], | |
| y = [0, norm.pdf(-1.5)], | |
| name = "Critical Value", | |
| mode = "lines+text", | |
| text = ["\\;z_{\\alpha}"], | |
| textposition = 'top right', | |
| textfont = Font( | |
| family = "sans serif", | |
| ), | |
| line = Line( | |
| shape = 'vh' | |
| ) | |
| ) | |
| trace3 = Scatter( | |
| x = np.linspace(-3, -1.5), | |
| y = norm.pdf(np.linspace(-3, -1.5)), | |
| name = 'Rejection Region', | |
| fill = 'tozeroy' | |
| ) | |
| layout = Layout( | |
| title = "Density Function", | |
| xaxis = XAxis( | |
| title = "z" | |
| ), | |
| yaxis = YAxis( | |
| title = "\\phi\\left(\\frac{\\bar{x}-\\theta_0}{\\theta_0/\\sqrt{n}}\\right)" | |
| ), | |
| annotations = Annotations([ | |
| Annotation( | |
| x = -2.15, | |
| y = 0.025, | |
| xref = 'x', | |
| yref = 'y', | |
| text = '\\alpha', | |
| showarrow = True, | |
| arrowhead = 2, | |
| arrowsize = 0.5, | |
| ax = 0, | |
| ay = -30 | |
| )] | |
| ) | |
| ) | |
| data = Data([trace1, trace2, trace3]) | |
| fig = Figure(data = data, layout = layout) | |
| plot_url = py.plot(fig, filename = 'pdf') |