Multiple Random Variables Problems

To probability lovers, I just want to share (and discuss) few simple problems I solved in Chapter 4 of Casella, G. and Berger, R.L. (2002). Statistical Inference.

1. A random point $(X,Y)$ is distributed uniformly on the square with vertices $(1, 1),(1,-1),(-1,1),$ and $(-1,-1)$. That is, the joint pdf is $f(x,y)=\frac{1}{4}$ on the square. Determine the probabilities of the following events.
   1. $X^2 + Y^2 < 1$
   2. $2X-Y>0$
   3. $|X+Y|<1$ (modified since the original $|X+Y|<2$ is trivial.)
   Solutions:
   1. $X^2 + Y^2 < 1$
      We need to consider the boundary of this inequality first in the unit square, so below is the plot of $X^2 + Y^2 = 1$,
      
      
      Hence, we are interested in the area of the ellipse above since $X^2 + Y^2$ is less than 1. To compute the area of the ellipse, notice that the regions in the 4 quadrants are identical except on the orientation, thus we can compute the area of the first quadrant then we simply multiply this by 4 to cover the overall area of the said geometric. \begin{equation}\nonumber \begin{aligned} P(X^2 + Y^2 < 1) &= 4\int_{0}^{1}\int_{0}^{\sqrt{1 - x^2}}\frac{1}{4}\operatorname{d}y\operatorname{d}x\\ &= \int_{0}^{1}y\Bigg|_{y=0}^{y=\sqrt{1 - x^2}}\operatorname{d}x = \int_{0}^{1}\sqrt{1 - x^2}\operatorname{d}x\\ &=\left(\frac{x}{2} \sqrt{- x^{2} + 1} + \frac{1}{2} \operatorname{sin}^{-1}{\left (x \right )}\right)\Bigg|_{x=0}^{x=1}\\ &=\frac{\pi}{4}-0=\frac{\pi}{4}. \end{aligned} \end{equation} Confirm this using python symbolic computation,
      
      
   2. Given $2X-Y>0$, we have
      \begin{equation}\nonumber P(2X-Y>0)=P(-Y>-2x) = P(Y<2X) \end{equation} The plot of $Y=2X$ is shown below,
      
      
      The shaded region is the event we are interested in, then \begin{equation}\nonumber \begin{aligned} P(Y < 2X) &= \int_{-1}^{1}\int_{\frac{y}{2}}^{1}\frac{1}{4}\operatorname{d}x\operatorname{d}y=\int_{-1}^{1}\frac{y}{4}\Bigg|_{\frac{y}{2}}^{1}\operatorname{d}y\\ &=\int_{-1}^{1}\left(\frac{1}{4}-\frac{y}{8}\right)\operatorname{d}y=\left(\frac{y}{4}-\frac{y^2}{16}\right)\Bigg|_{-1}^{1}\\ &=\left(\frac{1}{4}-\frac{1}{16}\right)-\left(-\frac{1}{4}-\frac{1}{16}\right)=\frac{1}{2}. \end{aligned} \end{equation}
   3. Given $|X+Y| < 1$, we have \begin{equation}\nonumber P(|X+Y|<1) = P(-1 < X+Y < 1) = P(-1-X < Y < 1-X) \end{equation} The shaded region of both equations ($Y=1-X$ and $Y=-1-X$) is shown below
      
      
      Hence, we have \begin{equation}\nonumber \begin{aligned} P(-1-X < Y < 1-X) &= 2\int_{0}^{1}\int_{-1}^{1-x}\frac{1}{4}\operatorname{d}y\operatorname{d}x\\ &=\int_{0}^{1}\frac{y}{2}\Bigg|_{-1}^{1-x}\operatorname{d}x=\int_{0}^{1}\left(\frac{1-x}{2}+\frac{1}{2}\right)\operatorname{d}x\\ &=\left(x-\frac{x^2}{4}\right)\Bigg|_{0}^{1}=\frac{3}{4}. \end{aligned} \end{equation}
2. A pdf is defined by \begin{equation}\nonumber f(x,y) = \begin{cases} C (x+2y) & \text{if}\;0 < y < 1\;\text{and}\;0 < x < 2\\ 0 & \text{otherwise}. \end{cases} \end{equation}
   1. Find the value of $C$.
   2. Find the marginal distribution of $X$.
   3. Find the joint cdf of $X$ and $Y$.
   Solutions:
   1. Find the value of $C$.
      To solve for the value of $C$ we integrate the given pdf first for $x$ and $y$, that is \begin{equation}\nonumber \begin{aligned} 1&=\int_{0}^{1}\int_{0}^{2}C (x+2y)\operatorname{d}x\operatorname{d}y= C\int_{0}^{1} \left(\frac{x^2}{2}+2xy\right)\Bigg|_{x=0}^{x=2}\operatorname{d}y\\ &=C\int_{0}^{1}(2+4y)\operatorname{d}y=C\left(2y+4\frac{y^2}{2}\right)\Bigg|_{y=0}^{y=1}\\ 1&=4C\Rightarrow C=\frac{1}{4} \end{aligned} \end{equation}
   2. Find the marginal distribution of $X$. \begin{equation}\nonumber \begin{aligned} f_X(x)&=\int_{0}^{1}f(x,y)\operatorname{d}y = \frac{1}{4}\int_{0}^{1}(x+2y)\operatorname{d}y\\ &=\frac{1}{4}(xy+y^2)\Bigg|_{y=0}^{y=1}=\begin{cases} \frac{1}{4}(x+1),&0 < x < 2\\ 0,&\text{elsewhere} \end{cases} \end{aligned} \end{equation}
   3. Find the joint cdf of $X$ and $Y$. \begin{equation}\nonumber \begin{aligned} F_{XY}(x,y)&=P(X\leq x, Y\leq y) = \frac{1}{4}\int_{0}^{x}\int_{0}^{y}(u+2v)\operatorname{d}v\operatorname{d}u\\ &=\frac{1}{4}\int_{0}^{x}(uv+v^2)\Bigg|_{v=0}^{v=y}\operatorname{d}u\\ &=\frac{1}{4}\int_{0}^{x}(uy+y^2)\operatorname{d}u\\ &=\frac{1}{4}\left(\frac{u^2y}{2}+uy^2\right)\Bigg|_{u=0}^{u=x}=\frac{x^2y}{8}+\frac{xy^2}{4} \end{aligned} \end{equation} If $x\geq 2$ and $0 < y < 1$, then \begin{equation}\nonumber \begin{aligned} F_{XY}(x,y)&=P(X\leq x, Y\leq y) = \frac{1}{4}\int_{0}^{2}\int_{0}^{y}(u+2v)\operatorname{d}v\operatorname{d}u\\ &=\frac{1}{4}\int_{0}^{2}(uv+v^2)\Bigg|_{v=0}^{v=y}\operatorname{d}u\\ &=\frac{1}{4}\int_{0}^{2}(uy+y^2)\operatorname{d}u\\ &=\frac{1}{4}\left(\frac{u^2y}{2}+uy^2\right)\Bigg|_{u=0}^{u=2}=\frac{y}{2}+\frac{y^2}{2} \end{aligned} \end{equation} If $0 < x < 2$ and $y \geq 1$, then \begin{equation}\nonumber \begin{aligned} F_{XY}(x,y)&=P(X\leq x, Y\leq y) = \frac{1}{4}\int_{0}^{x}\int_{0}^{1}(u+2v)\operatorname{d}v\operatorname{d}u\\ &=\frac{1}{4}\int_{0}^{x}(uv+v^2)\Bigg|_{v=0}^{v=1}\operatorname{d}u\\ &=\frac{1}{4}\int_{0}^{x}(u+1)\operatorname{d}u\\ &=\frac{1}{4}\left(\frac{u^2}{2}+u\right)\Bigg|_{u=0}^{u=x}=\frac{x^2}{8}+\frac{x}{4} \end{aligned} \end{equation}
   Hence below is the summary of the cdf, \begin{equation}\nonumber F_{XY}(x,y)=\begin{cases} 0,&x\leq 0, y\leq 0\\ \frac{x^2y}{8}+\frac{xy^2}{4},& 0 < x < 2\;\text{and}\;0 < y < 1\\ \frac{y}{2}+\frac{y^2}{2},& x\geq 2\;\text{and}\;0 < y < 1\\ \frac{x^2}{8}+\frac{x}{4}, & 0 < x < 2\;\text{and}\;y \geq 1\\ 1,&x\geq 2\;\text{and}\;y\geq 1 \end{cases} \end{equation}
3. 1. Find $P(X > \sqrt{Y})$ if $X$ and $Y$ are jointly distributed with pdf \begin{equation} f(x,y)=x+y,\;0\leq x\leq 1,\;0\leq y\leq 1. \end{equation}
   2. Find $P(X^2 < Y < X)$ if $X$ and $Y$ are jointly distributed with pdf \begin{equation} f(x,y)=2x,\;0\leq x\leq 1,\; 0\leq y \leq 1. \end{equation}
   Solutions:
   1. $P(X > \sqrt{Y})=P(Y < X^2)$. Now the plot of $y=x^2$ is shown below
      
      
      The probability of the blue region above is computed as follows, \begin{equation}\nonumber \begin{aligned} P(Y < X^2)&=\int_{0}^{1}\int_{0}^{x^2}x + y\operatorname{d}y\operatorname{d}x\\ &=\int_{0}^{1}\left(xy+\frac{y^2}{2}\right)\Bigg|_{y=0}^{y=x^2}\operatorname{d}x\\ &=\int_{0}^{1}\left(x^3+\frac{x^4}{2}\right)\operatorname{d}x\\ &=\left(\frac{x^4}{4}+\frac{x^5}{10}\right)\Bigg|_{0}^{1}\\ &=\frac{1}{4}+\frac{1}{10}=\frac{7}{20} \end{aligned} \end{equation}
   2. So we are interested on the event between $y=x$ and $y=x^2$, as shown below
      
      
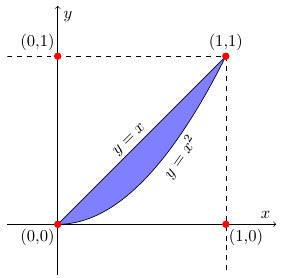
      Thus, \begin{equation}\nonumber \begin{aligned} P(X^2 < Y < X) &=\int_{0}^{1}\int_{x^2}^{x}2x\operatorname{d}y\operatorname{d}x\\ &=\int_{0}^{1}2xy\Bigg|_{y=x^2}^{y=x}\operatorname{d}x=\int_{0}^{1}(2x^2-2x^3)\operatorname{d}x\\ &=\left(\frac{2x^3}{3}-\frac{x^4}{2}\right)\Bigg|_{0}^{1}\\ &=\frac{2}{3}-\frac{1}{2}=\frac{1}{6} \end{aligned} \end{equation}